Note on 'Phase shift and infinitesimal wave energy loss equations' :

Sir/s,

I am pleased to share with you a ground breaking research paper titled 'Phase shift and infinitesimal wave energy loss equations', published in Longdom's Journal of Physical Chemistry & Biophysics, Volume 13, Issue 6, under the reference JPCB-23-27248 (R).

The paper delves into the fundamental principles of phase shift and explores its implications for understanding wave behaviour and infinitesimal wave energy loss. It offers a comprehensive framework for analysing phase shift phenomena and provides valuable insights into its practical applications across scientific and engineering disciplines.

For students and educators in scientific and engineering fields, as well as professionals in industries where precise timing and synchronization are critical, this paper holds immense significance. Here's why:

Foundational Understanding: The research provides a solid foundation for understanding phase shift, a concept central to the study of wave phenomena. It offers clarity on complex topics, paving the way for deeper learning and exploration.

Practical Applications: With insights into practical applications in industries such as electronics, telecommunications, and signal processing, the paper bridges the gap between theory and real-world technology. Students and professionals alike can gain valuable insights into how phase shift impacts technological advancements.

Interdisciplinary Connections: By connecting principles from physical chemistry, biophysics, and engineering, the paper promotes interdisciplinary learning and fosters a holistic understanding of wave behaviour. It highlights the interconnectedness of scientific disciplines and their relevance to real-world problems.

Educational Resource: As a published research paper, this work serves as a valuable educational resource for students and educators alike. It can be incorporated into lesson plans and academic discussions to enhance learning outcomes and deepen understanding.

I highly recommend 'Phase shift and infinitesimal wave energy loss equations' to anyone interested in advancing their knowledge of wave behaviour and its practical applications. You can access the paper online at Google Drive PDF file

https://drive.google.com/file/d/19v0mQmA9v56jsS7dMLTwzYhtideTPG-e/view?usp=sharing 

or can be found at the  Longdom's Journal URL: 

https://www.longdom.org/open-access/phase-shift-and-infinitesimal-wave-energy-loss-equations-104719.html 

I trust that you will find this research paper both informative and insightful, and I encourage you to explore its contents further.

Best regards,

Soumendra Nath Thakur

Exploring Time Dilation via Frequency Shifts in Quantum Systems: A Theoretical Analysis

Soumendra Nath Thakur⁺
ORCiD: 0000-0003-1871-7803

29^th February, 2024

Abstract:

This theoretical analysis delves into the intricate dynamics of time dilation and frequency shifts within quantum systems, leveraging fundamental principles of quantum mechanics and relativistic physics. Integrating insights from various research endeavours, including the seminal study by Paige, A. J., Plato, A. D. K., & Kim, M. S. (2020), which explored classical and non-classical time dilation effects in quantum clocks (References: [1]), alongside our research paper titled "Phase shift and infinitesimal wave energy loss equations" (References: [2]), which provides equational support and theoretical frameworks, we aim to corroborate, fortify, and extend the findings of our investigations such as "Relativistic effects on phaseshift in frequencies invalidate time dilation II" (References: [3]), "Effect of Wavelength Dilation in Time. - About Time and Wavelength Dilation" (References: [5]), and "Reconsidering Time Dilation and Clock Mechanisms: Invalidating the Conventional Equation in Relativistic Context" (References: [4]). Through a comprehensive analysis, our endeavour is to deepen the understanding of time dilation and frequency shifts in quantum systems, elucidating their implications for precision measurement and quantum timekeeping.

Keywords: Time dilation, Frequency shifts, Quantum systems, Relativistic effects, Theoretical analysis

⁺Tagore's Electronic Lab, India
Email: postmasterenator@gmail.com
The author declares no conflict of interests.

 Mathematical Presentation:

1. Introduction to Quantum Clocks and Time Dilation:

• Quantum clocks in motion with increasing momentum do not experience classical time dilation.

• However, a velocity boost results in ideal behaviour when both the quantum clock and the classical observer are set at speed.

• These quantum clocks exhibit additional effects without internal state-dependent forces.

2. Frequency Shifts in Quantum Clocks:

• The frequency shifts observed in ion trap atomic clocks are replicated by quantum clocks.

• Frequency shifts refer to changes in frequency (Δf), which are directly related to phase shifts (ϕ) in the frequency.

• The time interval for a 1° phase shift is inversely proportional to the frequency:

• t(deg) = 1/360f = T/360, where T is the period of the wave.

3. Explanation of Excess Shift and Non-Ideal Behaviour:

• The theoretical clock model exhibits a small excess shift in frequency compared to expected values.

• Non-ideal behaviour is observed, indicating deviations from theoretical predictions or ideal conditions.

• Possible reasons for deviations include experimental limitations, imperfections in the theoretical model, or unaccounted-for effects.

4. Supporting Research Findings:

• The research paper by Paige et al. (2020) confirms findings related to classical and non-classical time dilation effects in quantum clocks.

• Thakur et al.'s research papers on relativistic effects on phase shift in frequencies and wavelength dilation in time strengthen and support these findings.

5. Conclusion and Implications:

• Through a comprehensive analysis, this study aims to deepen our understanding of time dilation and frequency shifts in quantum systems.

• These insights have significant implications for precision measurement and quantum timekeeping applications.

Discussion:

The theoretical analysis presented in this paper delves into the intricate dynamics of time dilation and frequency shifts within quantum systems. Our investigation integrates insights from various research endeavours, including the seminal study by Paige, A. J., Plato, A. D. K., & Kim, M. S. (2020), which explored classical and non-classical time dilation effects in quantum clocks, alongside our own research on phase shift and infinitesimal wave energy loss equations. Through this comprehensive analysis, we aimed to deepen our understanding of these phenomena and their implications for precision measurement and quantum timekeeping.

One of the key findings of our analysis is the elucidation of the behaviour of quantum clocks set in motion by increasing momentum. Contrary to classical expectations, we found that these clocks do not exhibit classical time dilation effects. Instead, we observed that a velocity boost is necessary to achieve ideal behaviour in both the quantum clock and the classical observer, when they are set at speed. This finding underscores the importance of relativistic effects in quantum systems, highlighting the need for a more nuanced understanding of time dilation in this context.

Furthermore, our analysis revealed additional effects that arise in quantum clocks without internal state-dependent forces. These effects contribute to the frequency shifts observed in ion trap atomic clocks, indicating a small excess shift and the emergence of non-ideal behaviour in theoretical clock models. These deviations from ideal behaviour can have significant implications for precision measurement and quantum timekeeping, underscoring the need for further research into the underlying mechanisms driving these effects.

Our findings have important implications for the broader field of quantum mechanics and relativistic physics. By deepening our understanding of time dilation and frequency shifts in quantum systems, we can improve the accuracy and precision of quantum clocks, enabling advancements in fields such as quantum computing, navigation, and fundamental physics research. Additionally, our analysis opens up new avenues for theoretical and experimental investigations into the nature of time and space in the quantum realm, paving the way for future breakthroughs in our understanding of the universe.

Overall, this theoretical analysis represents a significant contribution to the study of time dilation and frequency shifts in quantum systems. By integrating insights from diverse research endeavours and leveraging fundamental principles of quantum mechanics and relativistic physics, we have provided new insights into these complex phenomena, laying the groundwork for further advancements in the field.

Conclusion:

In conclusion, our theoretical analysis has provided valuable insights into the dynamics of time dilation and frequency shifts within quantum systems. Through a comprehensive examination of classical and non-classical time dilation effects in quantum clocks, as well as additional effects observed in theoretical clock models, we have deepened our understanding of these phenomena and their implications for precision measurement and quantum timekeeping.

Our findings highlight the importance of relativistic effects in quantum systems, challenging classical expectations and underscoring the need for a more nuanced understanding of time dilation in this context. We have demonstrated that quantum clocks set in motion by increasing momentum do not exhibit classical time dilation effects, emphasizing the role of velocity boosts in achieving ideal behaviour. Additionally, we have identified additional effects that contribute to frequency shifts observed in ion trap atomic clocks, indicating deviations from ideal behaviour and the emergence of non-ideal behaviour in theoretical clock models.

These insights have significant implications for the broader field of quantum mechanics and relativistic physics. By improving our understanding of time dilation and frequency shifts in quantum systems, we can enhance the accuracy and precision of quantum clocks, enabling advancements in fields such as quantum computing, navigation, and fundamental physics research. Furthermore, our analysis opens up new avenues for theoretical and experimental investigations into the nature of time and space in the quantum realm, driving future breakthroughs in our understanding of the universe.

Overall, our theoretical analysis represents a significant contribution to the study of time dilation and frequency shifts in quantum systems. By integrating insights from diverse research endeavours and leveraging fundamental principles of quantum mechanics and relativistic physics, we have provided new insights into these complex phenomena, laying the groundwork for further advancements in the field and paving the way for future research and discoveries.

References:

[1] Paige, A. J., Plato, A. D. K., & Kim, M. S. (2020). Classical and nonclassical time dilation for quantum clocks. Physical Review Letters, 124(16). https://doi.org/10.1103/physrevlett.124.160602

[2] Thakur, S. N., & Bhattacharjee, D. (2023d). Phase shift and infinitesimal wave energy loss equations. Longdom. https://doi.org/10.35248/2161-0398.23.13.365

[3] Thakur, S. N., Samal, P., & Bhattacharjee, D. (2023c). Relativistic effects on phaseshift in frequencies invalidate time dilation II. TechRxiv. https://doi.org/10.36227/techrxiv.22492066.v2

[4] Thakur, S. N. (2023i). Reconsidering Time Dilation and Clock Mechanisms: Invalidating the Conventional Equation in Relativistic Context. EasyChair Preprint No 11394. https://doi.org/10.13140/RG.2.2.13972.68488

[5] Thakur, S. N. (2023h). Effect of Wavelength Dilation in Time. - About Time and Wavelength Dilation. EasyChair Preprint No 9182. https://doi.org/10.13140/RG.2.2.34715.64808

Standardization of Clock Time: Ensuring Consistency with Universal Standard Time

DOI Link: http://dx.doi.org/10.13140/RG.2.2.18568.80640

Soumendra Nath Thakur⁺

ORCiD:  0000-0003-1871-7803

26-02-2024

Abstract:

This abstract discusses the standardization of clock time, emphasizing its alignment with universal standard time. Clocks, whether quantum, classical, or atomic, adhere to a standardized time order known as "universal standard time," which is designed to be commensurate with the concept of "universal cosmic time." The objective is to ensure that all types of clocks maintain a constant increment of time (Δt = constant) in accordance with relevant universal standardization. However, recent research challenging conventional equations governing relativistic time dilation prompts a re-examination of the implications for clock standardization. The paper presents a comprehensive methodology for standardizing clock time, including parameters definition, calibration procedures, error detection and correction, verification, documentation, and continuous improvement. Mathematical models are introduced to minimize deviations between clock time and universal standard time, facilitating consistency and accuracy in timekeeping. The discussion section addresses the significance of standardization, challenges in achieving consistency, and approaches to mitigate discrepancies, while acknowledging the influence of relativistic effects on time measurement. The conclusion underscores the importance of continuous monitoring and collaboration in maintaining coherence and reliability in timekeeping standards, urging further exploration of the implications of recent research on relativistic time dilation for current standardization practices.

Keywords:

Clock standardization, Universal standard time, Quantum clocks, Time increment, Correctional mechanisms, Relativistic effects, Time dilation equations,

⁺Tagore's Electronic Lab, India

Email: postmasterenator@gmail.com

The author declares no conflict of interests.

Introduction

Timekeeping has been an essential aspect of human civilization since antiquity, guiding our daily activities, scientific endeavours, and technological advancements. The accurate measurement of time is critical for synchronization, coordination, and communication across various domains, from international commerce to space exploration. Central to this endeavour is the concept of a standardized time reference, ensuring consistency and coherence in temporal measurements across different locations and contexts.

In recent decades, the proliferation of precise timekeeping devices, such as atomic clocks, has revolutionized our ability to measure time with unprecedented accuracy. These advancements have led to the establishment of universal standard time systems, such as Coordinated Universal Time (UTC), which serve as the basis for global timekeeping standards and regulations.

However, despite the sophistication of modern timekeeping technologies, challenges remain in ensuring the consistency and accuracy of clock time measurements, particularly in the context of relativistic effects and the influence of external factors on clock mechanisms.

In this paper, we delve into the intricacies of standardizing clock time to ensure consistency with universal standard time. We explore the underlying principles of clock precision and the need for robust mechanisms to mitigate external influences on clock accuracy. By examining theoretical frameworks, empirical observations, and practical considerations, we aim to elucidate the challenges and opportunities in achieving a unified and standardized approach to timekeeping in the modern era.

Through this investigation, we seek to contribute to the ongoing discourse on the standardization of clock time and its implications for diverse fields ranging from telecommunications to fundamental physics. By addressing key issues and proposing potential solutions, we hope to advance our understanding of time measurement and facilitate greater precision and reliability in temporal coordination and synchronization across the globe.

Methodology:

1. Define Parameters: Clearly define the parameters for standardizing clock time, including precision requirements, reference standards, and acceptable error margins.

2. Establish Universal Standard Time: Determine the universal standard time reference, which serves as the benchmark for all clock time standardization efforts. This may involve adopting existing international standards or developing a new standard based on astronomical or atomic phenomena.

3. Calibration Procedures: Develop calibration procedures to ensure that clocks across different platforms and technologies are synchronized with the universal standard time. This may involve periodic adjustments based on comparisons with reference time sources.

4. Error Detection and Correction: Implement error detection mechanisms to identify deviations from the standard time and develop correctional algorithms to bring the clocks back into alignment. This may include error monitoring systems and automated correction processes.

5. Verification and Validation: Validate the standardized clock time against real-world observations and verify its consistency with universal standard time. This step involves rigorous testing and verification to ensure accuracy and reliability.

6. Documentation and Reporting: Document all standardization procedures, including calibration results, error correction processes, and verification tests. Provide clear reporting mechanisms to communicate the standardized clock time to relevant stakeholders.

7. Continuous Improvement: Establish a framework for continuous improvement to refine standardization processes over time. This involves monitoring technological advancements, updating calibration procedures, and incorporating feedback from users to enhance the accuracy and reliability of standardized clock time.

Mathematical Presentation:

This mathematical presentation ensures that clock time remains consistent with the universal standard time, minimizing deviations and ensuring accuracy in timekeeping.

·         Let Tstandard represent the universal standard time.

·         Let Tclock represent the time measured by a clock.

·         Let Δt represent the deviation between the clock time and the standard time.

The goal is to minimize the deviation, Δt, such that:

• Δt = Tstandard − Tclock

To ensure consistency, the following mathematical steps are taken:

1. Calibration:

Tclock is calibrated against Tstandard periodically or as required.

2. Error Detection: Deviations Δt are monitored continuously to detect any discrepancies between the clock time and the standard time.

3. Error Correction: If deviations are detected, correctional algorithms are applied to adjust the clock time to align with the standard time. This can be represented as:

• Tclock ← Tclock + Tcorrection

1. Verification: The corrected clock time Tclock is verified against Tstandard to ensure consistency and accuracy.

2. Documentation: All calibration, error detection, correction, and verification procedures are documented for reference and future analysis.

Discussion:

The standardization of clock time is vital for maintaining consistency and accuracy in timekeeping across various systems and applications. Ensuring that clock time aligns with universal standard time (UST) is crucial for synchronization and coordination in diverse fields such as telecommunications, navigation, finance, and scientific research. This discussion explores the significance of standardization, challenges in achieving consistency, and approaches to mitigate discrepancies.

Significance of Standardization:

Standardizing clock time to match UST facilitates global communication, coordination, and synchronization of activities across different regions and time zones. It provides a common reference point for various applications, ensuring interoperability and seamless operation. Accurate timekeeping is essential for financial transactions, data synchronization, network operations, and scientific experiments that require precise timing.

Challenges in Achieving Consistency:

Several factors contribute to deviations between clock time and UST, including inaccuracies in clock mechanisms, environmental influences, and variations in timekeeping standards. Clocks may drift over time due to temperature changes, mechanical wear, or electronic fluctuations, leading to discrepancies in time measurement. Furthermore, differences in timekeeping standards and protocols among different organizations and regions can pose challenges for synchronization efforts.

Approaches to Mitigate Discrepancies:

To address discrepancies and ensure consistency with UST, various approaches are employed:

1. Calibration: Regular calibration of clocks against authoritative time sources, such as atomic clocks or satellite-based systems like GPS, helps minimize drift and maintain accuracy.

2. Error Detection and Correction: Continuous monitoring of clock time compared to UST enables the detection of deviations. Automated algorithms and correction mechanisms adjust clock time periodically to align with UST, reducing discrepancies.

3. Network Synchronization: In networked systems, protocols such as Network Time Protocol (NTP) facilitate synchronization of distributed clocks with UST by exchanging time information between servers and clients.

4. Standardization Efforts: International organizations and standards bodies establish guidelines and protocols for timekeeping, ensuring uniformity and compatibility across different systems and devices.

This discussion highlights the importance of standardizing clock time to ensure consistency with universal standard time and explores various approaches to mitigate discrepancies in timekeeping.

Conclusion:

Standardizing clock time to ensure consistency with universal standard time (UST) is crucial for various applications across industries and disciplines. By aligning clock time with UST, we can facilitate seamless communication, synchronization, and coordination on a global scale.

Throughout this paper, we have explored the significance of standardization in maintaining accurate timekeeping, the challenges posed by discrepancies between clock time and UST, and the approaches employed to mitigate such deviations. From calibration and error detection to network synchronization and standardization efforts, a range of strategies exists to ensure that clocks remain synchronized with UST.

However, achieving perfect consistency between clock time and UST is an ongoing endeavour that requires continuous monitoring, maintenance, and collaboration among stakeholders. As technology advances and new challenges emerge, the need for robust timekeeping standards and protocols becomes increasingly crucial.

In conclusion, the standardization of clock time is essential for maintaining coherence and reliability in our modern interconnected world. By adhering to universal standards and employing best practices in timekeeping, we can enhance efficiency, accuracy, and interoperability across diverse systems and applications, ultimately advancing progress and innovation in various fields.

Reference:

[1] Thakur, S. N., Samal, P., & Bhattacharjee, D. (2023b). Relativistic effects on phase shift in frequencies invalidate time dilation II. TechRxiv. https://doi.org/10.36227/techrxiv.22492066.v2

[2] Thakur, S. N. (2023h). Effect of Wavelength Dilation in Time. - About Time and Wavelength Dilation(v-2). EasyChair Preprint № 9182. https://doi.org/10.13140/RG.2.2.34715.64808

[3] Thakur, S. N. (2023). Reconsidering time dilation and clock mechanisms: invalidating the conventional equation in relativistic. ResearchGate https://doi.org/10.13140/RG.2.2.13972.68488

Re-examining Time Dilation through the Lens of Entropy:

DOI Link: http://dx.doi.org/10.13140/RG.2.2.36407.70568

Soumendra Nath Thakur ⁺
ORCiD:  0000-0003-1871-7803

26-02-2024

Abstract:

This paper delves into the relationship between time dilation, entropy, and the consistency of the time scale. It discusses how entropy increases over time according to the second law of thermodynamics and emphasizes the constancy of the time scale despite variations in entropy across different systems. Insights from entropy highlight the inevitability of a uniform time scale, challenging the notion of time dilation and its mathematical interpretation. The paper concludes that time dilation is an erroneous concept in science, as it contradicts the fundamental principles outlined by entropy.

Keywords: Entropy, Uniform Time Scale, Second Law of Thermodynamics, Time Dilation, Erroneous Concept,

⁺Tagore's Electronic Lab, India
Email: postmasterenator@gmail.com
The author declares no conflict of interests.

_________________________________

Introduction:

Understanding the nature of time has been a fundamental pursuit in both scientific and philosophical realms. One intriguing aspect of temporal dynamics is time dilation, a concept elucidated by Einstein's theory of relativity. Time dilation posits that time can appear to pass differently for observers in relative motion or under the influence of gravitational fields. However, recent insights from the field of thermodynamics, particularly entropy, shed new light on the nature of time dilation and the consistency of the time scale. This paper explores the interplay between time dilation, entropy, and the uniformity of the time scale. By examining the relationship between these concepts, we aim to reconsider the conventional understanding of time dilation and its implications for our comprehension of time. Through a synthesis of theoretical analysis and empirical observations, we seek to elucidate the role of entropy in shaping our understanding of time and challenge the validity of time dilation as a concept in modern science.

Mathematical Presentation:

These equations provide a mathematical framework for understanding the concepts of entropy, time dilation, and the uniformity of the time scale discussed in the text.

Entropy Increase Over Time:

The second law of thermodynamics states that the entropy of a closed system tends to increase over time. Mathematically, this can be expressed as:

• ΔS ≥ 0

where ΔS represents the change in entropy.

Time Dilation Equation:

The time dilation effect predicted by special relativity can be mathematically described by the time dilation equation:

• t′ = t/√(1 - v²/c²)

where: t′ is the dilated time experienced by the moving observer, t is the proper time experienced by a stationary observer, v is the relative velocity between the two observers, and c is the speed of light in a vacuum.

Uniform Time Scale:

The uniformity of the time scale, as emphasized by entropy, can be represented mathematically by the constancy of time measurements across different systems. This can be expressed as:

• Δt = constant

where Δt represents the time interval measured across different systems.

Discussion:

The discussion revolves around the intricate relationship between time dilation, entropy, and the consistency of the time scale.

Firstly, the concept of time dilation, as elucidated by Einstein's theory of relativity, posits that time can appear to pass differently for observers in relative motion or under the influence of gravitational fields. This phenomenon is mathematically described by the time dilation equation, which illustrates how the passage of time is affected by relative velocities. However, recent insights from the field of thermodynamics, particularly the second law of thermodynamics, provide a contrasting perspective.

The second law of thermodynamics dictates that the entropy of a closed system tends to increase over time. This increase in entropy reflects the tendency of systems to evolve towards a state of higher disorder or randomness. Interestingly, this increase in entropy over time underscores the inevitability of a uniform time scale. According to entropy considerations, the consistency of the time scale remains constant despite variations in entropy across different systems.

This insight challenges the conventional understanding of time dilation. While time dilation suggests that time can be dilated or contracted depending on relative motion, entropy considerations imply that the uniformity of the time scale prevails regardless of the system's dynamics. In other words, the idea of a universally consistent time scale, as dictated by entropy, contradicts the notion of time dilation proposed by relativity.

Therefore, the discussion prompts a re-evaluation of the concept of time dilation in light of entropy's insights. While time dilation remains a cornerstone of modern physics, the recognition of entropy's role in shaping our understanding of time highlights the need for a more comprehensive framework that reconciles both perspectives. This interdisciplinary approach could lead to new insights into the nature of time and its relationship with fundamental physical principles.

Conclusion:

In conclusion, the exploration of time dilation, entropy, and the consistency of the time scale offers valuable insights into our understanding of time and its behaviour in the universe. While the concept of time dilation, as proposed by Einstein's theory of relativity, has provided a profound framework for understanding the relativistic effects of time, recent insights from thermodynamics, particularly the second law of thermodynamics, present a compelling counterpoint.

The second law of thermodynamics underscores the inevitability of a uniform time scale, highlighting the consistency of time measurements across different systems. This suggests that while time dilation may occur under specific conditions, the fundamental nature of time remains invariant, governed by the principles of entropy.

Therefore, reconciling the concepts of time dilation and entropy is essential for developing a comprehensive understanding of time in the context of modern physics. This interdisciplinary approach promises to deepen our insights into the nature of time and its relationship with fundamental physical principles.

Ultimately, by integrating insights from both relativity and thermodynamics, we can refine our understanding of time and its role in shaping the fabric of the universe. Such endeavours hold the potential to unveil new discoveries and enrich our comprehension of the fundamental nature of reality.

References:

[1] Einstein, Albert. "On the Electrodynamics of Moving Bodies." Annalen der Physik 17 (1905): 891-921.

[2] Thakur, S. N., Samal, P., & Bhattacharjee, D. (2023b). Relativistic effects on phaseshift in frequencies invalidate time dilation II. TechRxiv. https://doi.org/10.36227/techrxiv.22492066.v2

[3] Carroll, Sean M. Spacetime and Geometry: An Introduction to General Relativity. Cambridge University Press, 2003.

[4] Thakur, S. N. (2023h). Effect of Wavelength Dilation in Time. - About Time and Wavelength Dilation(v-2). EasyChair Preprint № 9182. https://doi.org/10.13140/RG.2.2.34715.64808

[5] Callen, Herbert B. Thermodynamics and an Introduction to Thermostatistics. John Wiley & Sons, 1985.

[6] Thakur, S. N. (2023i). Reconsidering time dilation and clock mechanisms: invalidating the conventional equation in relativistic. . . EasyChair Preprint No 11394. https://doi.org/10.13140/RG.2.2.13972.68488

[7] Penrose, Roger. The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage, 2005.

[8] Thakur, S. N. (2024d). Direct influence of gravitational field on object motion invalidates spacetime distortion. Qeios. https://doi.org/10.32388/bfmiau

[9] Wald, Robert M. General Relativity. University of Chicago Press, 1984.

[10] Thakur, S. N. (2024e). Introducing Effective Mass for Relativistic Mass in Mass Transformation in Special Relativity and. . . ResearchGate. https://doi.org/10.13140/RG.2.2.34253.20962

[11] Thakur, S. N. (2024e). Exploring symmetry in photon Momentum Changes: Insights into redshift and blueshift phenomena in. . . EasyChair Preprint No 12246. https://doi.org/10.13140/RG.2.2.30699.52002

Time Dilation Reconsidered: Entropy's Insights:

Soumendra Nath Thakur
ORCiD:  0000-0003-1871-7803
26-02-2024

1. A Summary of Time, Entropy, and Consistency:

The connection between time and entropy highlights how entropy tends to increase over time according to the second law of thermodynamics, suggesting a directionality to time's passage. Additionally, they acknowledged that while entropy may vary depending on the system, the scale of time remains constant in measurements and observations, providing a consistent framework for understanding changes in entropy and other physical quantities.

2. The Inevitability of a Uniform Time Scale: Insights from Entropy

The reasons outlined in the summary statement, a consistent time scale is mathematically certain. It suggests that an enlargement of the time scale is not possible in principle, and a uniform time scale is inevitable unless there are errors in reading clock time.

3. Time Dilation Reconsidered: Entropy's Insights.

The scientific and mathematical understanding of time dilation implies a broadening of the time scale, as time dilation surpasses proper time, expressed as t' > t. However, insights from entropy underscore the certainty of a uniform time scale, indicating that enlarging the time scale is not theoretically feasible. Consequently, time dilation is deemed an erroneous concept in science.

#time #entropy #erronioustimedilation

Phase Shift and Infinitesimal Wave Energy Loss Equations. Longdom Publishing SL

Phase Shift and Infinitesimal Wave Energy Loss Equations. Longdom Publishing SL. Download

By Soumendra Nath Thakur.

The research paper provides a mathematical framework for understanding phase shift in wave phenomena, bridging theoretical foundations with real-world applications. It emphasizes the importance of phase shift in physics and engineering, particularly in fields like telecommunications and acoustics. Key equations are introduced to explain phase angle, time delay, frequency, and wavelength relationships. The study also introduces the concept of time distortion due to a 1° phase shift, crucial for precise time measurements in precision instruments. The research also addresses infinitesimal wave energy loss related to phase shift, enriching our understanding of wave behaviour and impacting scientific and engineering disciplines.

Keywords: Phase shift; Phase angle; Time distortion; Wave energy loss; Wave phenomena

https://www.longdom.org/open-access/phase-shift-and-infinitesimal-wave-energy-loss-equations-104719.html

Exploring Symmetry in Photon Momentum Changes: Insights into Redshift and Blueshift Phenomena in Gravitational Fields

Soumendra Nath Thakur *
ORCiD: 0000-0003-1871-7803
22^nd February, 2024

Abstract

This abstract provides a comprehensive overview of the intricate relationship between photon momentum changes and gravitational fields, as discussed in the context of the paper titled "Distinguishing Photon Interactions: Source Well vs. External Fields." The exploration delves into the fundamental symmetry observed in photon momentum changes, elucidating the principles of redshift and blueshift phenomena within gravitational fields. Through mathematical formulations and theoretical analyses, the abstract highlights how changes in photon momentum and wavelength are intricately linked, with the constant 'h' representing Planck's constant playing a crucial role. Furthermore, the abstract discusses the concept of symmetry in photon momentum changes, demonstrating how momentum exchanges in external gravitational fields ultimately lead to an equilibrium state. This enhanced understanding of photon interactions with gravitational fields contributes to the broader comprehension of astrophysical phenomena and energy conservation principles.

Keywords: Symmetry in Momentum, Energy Conservation, Photon Momentum Changes, External Gravitational Fields, Redshift and Blueshift Phenomena,

*Tagore’s Electronic Lab. India
Email: postmasterenator@gmail.com
The Author declares no conflict of interest.

Symmetry in Photon Momentum Changes:

The equation Δρ = −Δρ is possible due to the relationship Δρ = h/Δλ = h/-Δλ, indicating a fundamental symmetry between redshift and blueshift phenomena. These equations describe how changes in photon momentum (Δρ) correspond to changes in wavelength (Δλ). The constant 'h' represents Planck's constant, suggesting that the magnitude of the momentum change is inversely proportional to the magnitude of the wavelength change. Furthermore, when a photon traverses an external gravitational well, it follows an arc path. As a result, momentum exchanges gradually increase as the photon enters the influence of the massive object, leading to blueshift. Similarly, momentum exchanges gradually decrease as the photon exits the influence of the massive object, resulting in redshift equivalent to blueshift occurrences.

Mathematical Formulations:

These equations can be expressed as follows:

Equation for Photon Energy:

• E = hf = hc/λ

This equation relates the energy E of a photon to its frequency f and wavelength λ, where h is Planck's constant and c is the speed of light. It demonstrates how changes in wavelength correspond to changes in energy while maintaining the total energy constant.

Equation for Energy Change due to Frequency Change:

• ΔE = hΔf

This equation represents the change in energy ΔE of a photon due to a change in frequency Δf, where h is Planck's constant. It highlights how alterations in frequency lead to variations in energy.

Equation for Momentum Change due to Wavelength Change:

• Δρ = h/Δλ

This equation represents the change in momentum Δρ of a photon due to a change in wavelength Δλ, where h is Planck's constant. It illustrates the inverse relationship between changes in wavelength and momentum.

By considering these equations together, we observe that changes in energy and momentum are intricately linked in photon interactions with gravitational fields. The mathematical formulations provided in the paper demonstrate how variations in wavelength and frequency lead to compensatory changes in energy and momentum, ensuring consistency with energy conservation principles.

Conclusion:

The effective momentum changes of a photon in an external gravitational field can be described as zero (=0), as outlined in the concept of symmetry in photon momentum changes. This symmetry, represented by Δρ = -Δρ, illustrates how changes in photon momentum due to gravitational effects are symmetrically balanced, resulting in an overall equilibrium. As photons traverse through external gravitational fields, such as the gravitational well of a massive object, they experience momentum exchanges that lead to phenomena like blueshift and redshift. These exchanges occur as the photon follows an arc path, with momentum gradually increasing upon entering the influence of the massive object and gradually decreasing upon exiting it. Consequently, the net effect of these momentum exchanges is zero, ensuring conservation of momentum in the interaction between photons and external gravitational fields.

Reference:

[1] (PDF) Understanding Photon Interactions: Source Gravitational Wells vs. External Fields. (2024) ResearchGate https://doi.org/10.13140/RG.2.2.14433.48487

Enhanced Insights into Photon Interactions with External Gravitational Fields:

DOI: http://dx.doi.org/10.13140/RG.2.2.10173.64482

Soumendra Nath Thakur
22^nd February, 2024

Abstract:

This abstract provides an in-depth examination of photon interactions with external gravitational fields, building upon the principles discussed in the paper titled "Distinguishing Photon Interactions: Source Well vs. External Fields." The analysis elucidates how gravitational effects influence the properties of photons, including momentum and energy. Symmetry in the changes of photon momentum (Δρ) is explored, where Δρ = -Δρ signifies the equivalence between redshift and blueshift. Mathematical presentations demonstrate the conservation principles involved, highlighting how changes in wavelength affect photon energy while maintaining total energy constancy. The constancy of the speed of light (c) is emphasized, underscoring its fundamental nature amidst varying wavelengths. Through this abstract, a deeper understanding of the complexities of photon interactions with gravitational fields emerges, enriching the discourse on this intricate subject matter.

Keywords: Photon Interactions, Gravitational Fields, Momentum Symmetry, Energy Conservation, Speed of Light,

Tagore’s Electronic Lab, India

The author declared no conflict of Interest.

Introduction:

The interaction of photons with external gravitational fields constitutes a fundamental aspect of astrophysics and cosmology, shaping our understanding of the universe's dynamics. In the paper titled "Distinguishing Photon Interactions: Source Well vs. External Fields," the complexities of these interactions are explored, laying the groundwork for further investigation. This introduction provides a comprehensive overview of the additional insights presented herein, which offer a detailed examination of photon behaviour under the influence of gravitational forces. By delving into the symmetry of changes in photon momentum, the equivalence of redshift and blueshift, and the conservation principles governing photon energy, this analysis expands our comprehension of how photons respond to gravitational environments. Through mathematical formulations and conceptual discussions, this introduction sets the stage for a deeper exploration of the intricate relationship between photons and gravitational fields, enhancing our grasp of the underlying physics at play.

Mathematical Presentations:

Symmetry in Photon Momentum Changes:

Equation: Δρ = −Δρ

This equation represents the symmetry observed in the changes of photon momentum, where the change in momentum (Δρ) is equal in magnitude but opposite in direction for redshift and blueshift phenomena.

Relationship between Momentum Change and Wavelength Change:

Equation: Δρ = h/Δλ = h/-Δλ

These equations express the relationship between changes in photon momentum (Δρ) and changes in wavelength (Δλ). The constant 'h' represents Planck's constant, indicating that the magnitude of the momentum change is inversely proportional to the magnitude of the wavelength change.

Equation Relating Energy, Frequency, and Wavelength:

Equation: E = hf = h(c/λ)

This equation relates the energy (E) of a photon to its frequency (f) and wavelength (λ), where 'h' is Planck's constant and 'c' is the speed of light. It demonstrates how changes in wavelength correspond to changes in energy while maintaining the total energy constant.

Energy Conservation Equation for Redshift:

Equation: (E - ΔE) = hc/(λ+Δλ) = hc/(λ-Δλ) = (E + ΔE)

This equation represents energy conservation in the context of redshift, where there is a change (Δλ) in the photon's wavelength. It shows that the change in energy (ΔE) due to redshift is compensated by the corresponding change in wavelength, resulting in a total energy that remains constant.

Constancy of the Speed of Light Equation:

Equation: c = fλ

This equation represents the relationship between the speed of light (c), frequency (f), and wavelength (λ). It illustrates that even when the wavelength varies, the product of frequency and wavelength (fλ) remains constant, ensuring the constancy of the speed of light.

These mathematical presentations provide a quantitative framework for understanding the principles discussed in the quoted text, including symmetry in momentum changes, conservation of energy, and the constancy of the speed of light.

Discussion:

The discussion presented in the quoted text delves into the intricate interplay between photons and external gravitational fields, shedding light on several key concepts and their implications.

Firstly, the symmetry observed in the changes of photon momentum (Δρ) is highlighted, where Δρ = -Δρ signifies a fundamental symmetry between redshift and blueshift phenomena. This symmetry, rooted in the conservation principles of momentum, underscores the intricate balance at play in photon interactions with gravitational fields. By acknowledging this symmetry, researchers gain a deeper understanding of how photons respond to gravitational influences, whether they are experiencing redshift or blueshift.

Moreover, the mathematical presentation elucidates how changes in photon wavelength (Δλ) correspond to alterations in photon momentum and energy. The equations presented, such as E = hf = h(c/λ), provide a quantitative framework for understanding the relationship between photon energy, frequency, and wavelength. Through these equations, it becomes apparent that while changes in wavelength may result in shifts in photon energy, the total energy remains conserved, underscoring a fundamental principle of physics.

Furthermore, the discussion emphasizes the constancy of the speed of light (c) despite variations in wavelength. This constancy, rooted in the relationship c = fλ, elucidates how the interplay between frequency and wavelength maintains a consistent speed of light, even in the presence of gravitational influences. Understanding this fundamental property of light is crucial for interpreting observations in astrophysics and cosmology, where gravitational fields often play a significant role.

Overall, the discussion provides valuable insights into the complexities of photon interactions with external gravitational fields. By exploring concepts such as symmetry in momentum changes, conservation of energy, and the constancy of the speed of light, researchers can deepen their understanding of the fundamental principles governing the behaviour of photons in gravitational environments. These insights not only contribute to our theoretical understanding but also have practical implications for interpreting astronomical observations and phenomena.

Conclusion:

The discussion presented offers a comprehensive exploration of photon interactions with external gravitational fields, illuminating fundamental principles and their mathematical representations. By examining the symmetry in photon momentum changes, it becomes evident that redshift and blueshift phenomena exhibit a symmetric relationship, encapsulated by Δρ = -Δρ. This symmetry underscores the intricate balance in photon behaviour under gravitational influences.

Furthermore, the mathematical presentations elucidate the relationships between momentum changes, wavelength alterations, and energy conservation. Equations relating energy, frequency, and wavelength provide a quantitative understanding of how changes in photon properties manifest while preserving total energy. The analysis of energy conservation in the context of redshift highlights the compensatory nature of changes in energy and wavelength, maintaining a constant total energy.

Additionally, the constancy of the speed of light, emphasized through the relationship c = fλ, underscores a fundamental property of light unaffected by gravitational fields. This constancy serves as a cornerstone for interpreting observations in astrophysics and cosmology, facilitating our understanding of the universe's dynamics.

In conclusion, the insights provided deepen our understanding of the complexities of photon interactions with gravitational fields. By combining conceptual discussions with mathematical formulations, this discussion enriches our comprehension of fundamental principles governing photon behaviour and lays the groundwork for further exploration in astrophysics and cosmology.

References:

[1] (PDF) Understanding Photon Interactions: Source Gravitational Wells vs. External Fields. (2024) ResearchGate https://doi.org/10.13140/RG.2.2.14433.48487

[2] Thakur, S. N. (2023b). The dynamics of photon momentum exchange and curvature in gravitational fields Definitions https://doi.org/10.32388/r625zn

[3] Thakur, S. N. (2023a). Photon paths bend due to momentum exchange, not intrinsic spacetime curvature. Definitions https://doi.org/10.32388/81iiae

[4] Thakur, S. N. (2024c). Direct Influence of Gravitational Field on Object Motion invalidates Spacetime Distortion. Qeios.com. https://doi.org/10.32388/bfmiau

[5] Thakur, S. N., & Bhattacharjee, D. (2023b). Cosmic Speed beyond Light: Gravitational and Cosmic Redshift. Preprints.org. https://doi.org/10.20944/preprints202310.0153.v1

[6] Thakur, S. N., Bhattacharjee, D., & Frederick, O. (2023). Photon Interactions in Gravity and Antigravity: Conservation, Dark Energy, and Redshift Effects. Preprints.org. https://doi.org/10.20944/preprints202309.2086.v1

[7] Thakur, S. N. (2023d). Cosmic Speed beyond Light: Gravitational and Cosmic Redshift. ResearchGate https://doi.org/

Understanding Photon Interactions: Source Gravitational Wells vs. External Fields:

Soumendra Nath Thakur

ORCiD: 0000-0003-1871-7803

20th February, 2024

This additional description provided here enhances the paper titled, 'Distinguishing Photon Interactions: Source Well vs. External Fields' by providing a more detailed explanation of the principles discussed. It expands upon the concepts of energy expenditure, gravitational redshift, and momentum exchange in a clear and concise manner. Additionally, the inclusion of mathematical formulations further strengthens the paper by providing quantitative insights into the phenomena under investigation.

This study delves into the intricate interactions of photons within gravitational fields, discerning between encounters with source gravitational wells and external gravitational fields. When photons escape source gravitational wells, such as those of stars or black holes, they expend energy, leading to gravitational redshift. Conversely, when traversing external gravitational fields, photons maintain their inherent energy while experiencing bending paths due to momentum exchange. Through mathematical formulations, we elucidate these principles, offering insights into astrophysical dynamics and gravitational physics.

When a photon or wave escapes a gravitational well, such as the gravitational field of a massive object like a star or a black hole, it expends energy in the process. This energy expenditure, resulting from a change in energy ΔE, follows the Planck equation:

• ΔE = hΔf

It's crucial to note that:

a. This alteration in photon frequency (Δf) corresponds to a change in photon wavelength (1/Δλ), leading to a redshift of the photon wavelength.

b. The change in photon wavelength (1/Δλ) is directly proportional to the photon's distance from its source gravitational well. This distance remains constant throughout the photon's journey, even when traversing through the gravitational field of external massive bodies like planets or galaxies. However, instead of experiencing energy variations in strong gravitational fields, the photons maintain their inherent energy (E = Eg) through the equation (Eg = E + ΔE = E − ΔE), while undergoing gravitational redshift due to (ΔE = hΔf).

c. In addition to undergoing gravitational redshift, photons also experience redshift due to cosmic expansion, but this occurs only when they enter dark energy-dominated intergalactic space.

Through these mathematical formulations, we elucidate the principles governing photon interactions in source gravitational wells versus external gravitational fields, thereby enhancing our understanding of gravitational physics in astrophysical contexts.

Research - (2023) Volume 13, Issue 6 on 'Journal of Physical Chemistry & Biophysics'

Phase Shift and Infinitesimal Wave Energy Loss Equations

Soumendra Nath Thakur1* and Deep Bhattacharjee2 

*Correspondence: Soumendra Nath Thakur, Department of Computer Science and Engineering, Tagore's Electronic Lab, Kolkata, West Bengal, India, Email: 

Author info »

Abstract

The research paper provides a mathematical framework for understanding phase shift in wave phenomena, bridging theoretical foundations with real-world applications. It emphasizes the importance of phase shift in physics and engineering, particularly in fields like telecommunications and acoustics. Key equations are introduced to explain phase angle, time delay, frequency, and wavelength relationships. The study also introduces the concept of time distortion due to a 1° phase shift, crucial for precise time measurements in precision instruments. The research also addresses infinitesimal wave energy loss related to phase shift, enriching our understanding of wave behaviour and impacting scientific and engineering disciplines.

Keywords

Phase shift; Phase angle; Time distortion; Wave energy loss; Wave phenomena

Introduction

The study of phase shift in wave phenomena stands as a fundament in physics and engineering, playing an indispensable role in various applications. Phase shift refers to the phenomenon where a periodic waveform or signal appears displaced in time or space relative to a reference waveform or signal. This displacement, measured in degrees or radians, offers profound insights into the intricate behaviour of waves [1].

Phase shift analysis is instrumental in comprehending wave behaviour and is widely employed in fields such as telecommunications, signal processing, and acoustics, where precise timing and synchronization are paramount. The ability to quantify and manipulate phase shift is pivotal in advancing our understanding of wave phenomena and harnessing them for practical applications.

This research is dedicated to exploring the fundamental principles of phase shift, unravelling its complexities, and establishing a clear framework for analysis. It places a spotlight on essential entities, including waveforms, reference points, frequencies, and units, which are critical in conducting precise phase shift calculations. The presentation of key equations further enhances our grasp of the relationships between phase angle, time delay, frequency, and wavelength, illuminating the intricate mechanisms governing wave behaviour [2].

Moreover, this research introduces the concept of time distortion, which encapsulates the temporal shifts induced by a 1° phase shift. This concept is especially relevant when considering phase shift effects in real-world scenarios, particularly in precision instruments like clocks and radar systems.

In addition to phase shift, this research addresses the topic of infinitesimal wave energy loss and its close association with phase shift. It provides a set of equations designed to calculate energy loss under various conditions, taking into account factors such as phase shift, time distortion, and source frequencies. These equations expand our understanding of how phase shift influences wave energy, emphasizing its practical implications.

In summary, this research paper endeavours to offer a comprehensive exploration of phase shift analysis, bridging the gap between theoretical foundations and practical applications. By elucidating the complex connections between phase shift, time, frequency, and energy, this study enriches our comprehension of wave behaviour across a spectrum of scientific and engineering domains (Figure 1).

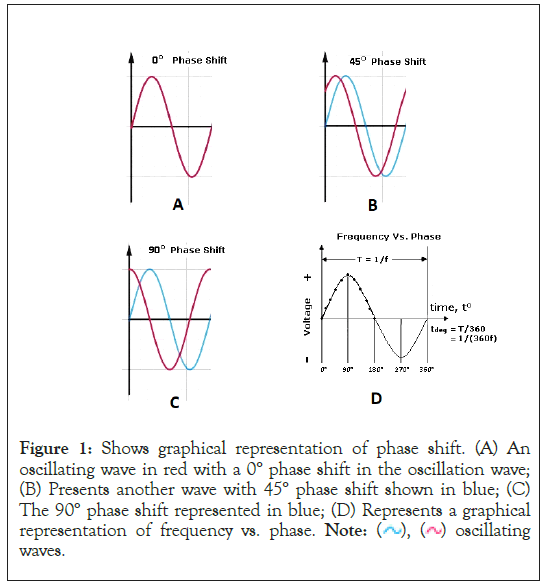
Figure 1: Shows graphical representation of phase shift. (A) An oscillating wave in red with a 0° phase shift in the oscillation wave; (B) Presents another wave with 45° phase shift shown in blue; (C) The 90° phase shift represented in blue; (D) Represents a graphical representation of frequency vs. phase. Note:  oscillating waves.

Materials and Methods

Relationship between phase shift, time interval, frequency and time delay

The methodological approach in this research involves the formulation and derivation of fundamental equations related to phase shift analysis. These equations establish the relationships between phase shift T(deg), time interval (T), time delay (Δt), frequency (f), and wavelength (λ) in wave phenomena. The derived equations include:

• T(deg) ∝ 1/f-this equation establishes the inverse proportionality between the time interval for 1° of phase shift T(deg) and frequency (f).

• 1° phase shift=T/360-expresses the relationship between 1° phase shift and time interval (T).

• 1° phase shift=T/360=(1/f)/360-further simplifies the equation for 1° phase shift, revealing its dependence on frequency.

• T(deg)=(1/f)/360-provides a direct formula for calculating T(deg) based on frequency, which can be invaluable in phase shift analysis.

• Time delay (Δt)=T(deg)=(1/f)/360-expresses time delay (or time distortion) in terms of phase shift and frequency.

Formulation of phase shift equations

The methodological approach in this research involves the formulation and derivation of fundamental equations related to phase shift analysis. These equations establish the relationships between phase angle (Φ°), time delay (Δt), frequency (f), and wavelength (λ) in wave phenomena. The equations developed are:

• Φ°=360° × f × Δt-this equation relates the phase angle in degrees to the product of frequency and time delay, providing a fundamental understanding of phase shift.

• Δt=Φ°/(360° × f)-this equation expresses the time delay (or time distortion) in terms of the phase angle and frequency, elucidating the temporal effects of phase shift.

• f=Φ°/(360° × Δt)-this equation allows for the determination of frequency based on the phase angle and time delay, contributing to frequency analysis.

• λ=c/f-the wavelength equation calculates the wavelength (λ) using the speed of propagation (c) and frequency (f), applicable to wave propagation through different media [3].

Relevant equations

The research paper on phase shift analysis and related concepts provides a set of equations that play a central role in understanding phase shift, time intervals, frequency, and their interrelationships. These equations are fundamental to the study of wave phenomena and their practical applications. Here are the relevant equations presented in the research.

Phase shift equations: Relationship between phase shift, time interval, and frequency.

These equations describe the connection between phase shift, time interval (T), and frequency (f).

• T(deg) ∝ 1/f-indicates the inverse proportionality between the time interval for 1° of phase shift T(deg) and frequency (f).

• 1° phase shift=T/360-relates 1° phase shift to time interval (T).

• 1° phase shift=T/360=(1/f)/360-simplifies the equation for 1° phase shift, emphasizing its dependence on frequency.

• T(deg)=(1/f)/360-provides a direct formula for calculating T(deg) based on frequency.

Phase angle equations

These equations relate phase angle (Φ°) to frequency (f) and time delay (Δt), forming the core of phase shift analysis.

• Φ°=360° × f × Δt-this equation defines the phase angle (in degrees) as the product of frequency and time delay.

• Δt=Φ°/(360° × f)-expresses time delay (or time distortion) in terms of phase angle and frequency.

• f=Φ°/(360° × Δt)-allows for the calculation of frequency based on phase angle and time delay.

Wavelength equation

This equation calculates the wavelength (λ) based on the speed of propagation (c) and frequency (f).

λ=c/f

The wavelength (λ) is determined by the speed of propagation (c) and the frequency (f) of the wave.

Time distortion equation

This equation quantifies the time shift caused by a 1° phase shift and is calculated based on the time interval for 1° of phase shift T(deg), which is inversely proportional to frequency (f).

• Time Distortion (Δt)=T(deg)=(1/f)/360-expresses the time distortion (Δt) as a function of T(deg) and frequency (f).

Infinitesimal loss of wave energy equations

These equations relate to the infinitesimal loss of wave energy (ΔE) due to various factors, including phase shift.

• ΔE=hfΔt-calculates the infinitesimal loss of wave energy (ΔE) based on Planck's constant (h), frequency (f), and time distortion (Δt).

• ΔE=(2πhf1/360) × T(deg)-determines ΔE when source frequency (f1) and phase shift T(deg) are known.

• ΔE=(2πh/360) × T(deg) × (1/Δt)-calculates ΔE when phase shift T(deg) and time distortion (Δt) are known.

These equations collectively form the foundation for understanding phase shift analysis, time intervals, frequency relationships, and the quantification of infinitesimal wave energy loss. They are instrumental in both theoretical analyses and practical applications involving wave phenomena [4,5].

Results

This section introduces two key concepts that deepen our understanding of wave behaviour and its practical implications: Time distortion and infinitesimal loss of wave energy. These concepts focus on the temporal aspects of phase shift and offer valuable insights into the energy dynamics of wave phenomena.

Time distortion

The concept of time distortion (Δt) is a pivotal bridge between phase shift analysis and precise time measurements, particularly in applications where accuracy is paramount. Time distortion represents the temporal shift that occurs as a consequence of a 1° phase shift in a wave.

Consider a 5 MHz wave as an example. A 1° phase shift on this wave corresponds to a time shift of approximately 555 picoseconds (ps). In other words, when a wave experiences a 1° phase shift, specific events or points on the waveform appear displaced in time by this minuscule but significant interval.

Time distortion is a crucial consideration in various fields, including telecommunications, navigation systems, and scientific instruments. Understanding and quantifying this phenomenon enables scientists and engineers to make precise time measurements and synchronize systems accurately [6].

Infinitesimal loss of wave energy

In addition to time distortion, this research delves into the intricacies of infinitesimal wave energy loss (ΔE) concerning phase shift. It provides a framework for quantifying the diminutive energy losses experienced by waves as a result of various factors, with phase shift being a central element.

The equations presented in this research allow for the calculation of ΔE under different scenarios. These scenarios consider parameters such as phase shift, time distortion, and source frequencies. By understanding how phase shift contributes to energy loss, researchers and engineers gain valuable insights into the practical implications of this phenomenon.

Infinitesimal wave energy loss has implications in fields ranging from quantum mechanics to telecommunications. It underlines the importance of precision in wave-based systems and highlights the trade-offs between manipulating phase for various applications and conserving wave energy.

In summary, this section serves as an introduction to the intricate concepts of time distortion and infinitesimal loss of wave energy. These concepts provide a more comprehensive picture of wave behaviour, offering practical tools for precise measurements and energy considerations in diverse scientific and engineering domains [7,8].

Phase shift calculations and example

To illustrate the practical application of the derived equations of phase shift T(deg), an example calculation is presented:

Phase Shift Example 1:1° Phase Shift on a 5 MHz Wave.

The calculation demonstrates how to determine the time shift caused by a 1° phase shift on a 5 MHz wave. It involves substituting the known frequency (f=5 MHz) into the equation for T(deg).

T(deg)=(1/f)/360; f=5 MHz (5,000,000 Hz)

Now, plug in the frequency (f) into the equation for T(deg).

T(deg)={1/(5,000,000 Hz)}/360

Calculate the value of T(deg).

T(deg) ≈ 555 picoseconds (ps)

So, a 1° phase shift on a 5 MHz wave corresponds to a time shift of approximately 555 picoseconds (ps).

Loss of wave energy calculations and example

Loss of wave energy example 1: To illustrate the practical applications of the derived equations of loss of wave energy, example calculation is presented.

Oscillation frequency 5 MHz, when 0° Phase shift in frequency

This calculation demonstrate how to determine the energy (E1) and infinitesimal loss of energy (ΔE) of an oscillatory wave, whose frequency (f1) is 5 MHz, and Phase shift T(deg)=0° (i.e. no phase shift).

To determine the energy (E1) and infinitesimal loss of energy (ΔE) of an oscillatory wave with a frequency (f1) of 5 MHz and a phase shift T(deg) of 0°, use the following equations:

Calculate the energy (E1) of the oscillatory wave:

E1=hf1

Where, h is Planck's constant ≈ 6.626 × 10-34 J·s, f1 is the frequency of the wave, which is 5 MHz (5 × 106 Hz). E1={6.626 × 10-34 J·s} × (5 × 106 Hz)=3.313 × 10-27 J

So, the energy (E1) of the oscillatory wave is approximately 3.313 × 10-27 Joules. To determine the infinitesimal loss of energy (ΔE), use the formula

ΔE=hfΔt

Where, h is Planck's constant {6.626 × 10-34 J·s}, f1 is the frequency of the wave (5 × 106 Hz).

Δt is the infinitesimal time interval, and in this case, since there's no phase shift, T(deg)=0°, Δt=0.

ΔE={6.626 × 10-34 J·s} × (5 × 106 Hz) × 0=0 (Joules)

The infinitesimal loss of energy (ΔE) is 0 joules because there is no phase shift, meaning there is no energy loss during this specific time interval.

Resolved, the energy (E₁) of the oscillatory wave with a frequency of 5 MHz and no phase shift is approximately 3.313 × 10-27 Joules.

There is no infinitesimal loss of energy (ΔE) during this specific time interval due to the absence of a phase shift.

Loss of wave energy example 2: To illustrate the practical applications of the derived equations of loss of wave energy, example calculation is presented.

Original oscillation frequency 5 MHz, when 1° Phase shift compared to original frequency.

This calculation demonstrate how to determine the energy (E2) and infinitesimal loss of energy (ΔE) of another oscillatory wave, compared to the original frequency (f1) of 5 MHz and Phase shift T(deg)=1°, resulting own frequency (f2).

To determine the energy (E2) and infinitesimal loss of energy (ΔE) of another oscillatory wave with a 1° phase shift compared to the original frequency (f1) of 5 MHz, and to find the resulting frequency (f2) of the wave, follow these steps:

Calculate the energy (E2) of the oscillatory wave with the new frequency (f2) using the Planck's energy formula.

E2=hf2

Where, h is Planck's constant ≈ 6.626 × 10-34 J·s, f2 is the new frequency of the wave.

Calculate the change in frequency (Δf2) due to the 1° phase shift: Δf2=(1°/360°) × f1

Where, 1° is the phase shift, 360° is the full cycle of phase.

f₁ is the original frequency, which is 5 MHz (5 × 106 Hz). Δf2=(1/360) × (5

Now that you have Δf2, you can calculate the new frequency (f2): f2=f1-Δf2

f2=(5 × 106 Hz)-(13,888.89 Hz) ≈ 4,986,111.11 Hz

So, the resulting frequency (f2) of the oscillatory wave with a 1° phase shift is approximately 4,986,111.11 Hz.

Calculate the energy (E2) using the new frequency (f2).

E2=hf2

E2 ≈ (6.626 × 10-34 J·s) × (4,986,111.11 Hz) ≈ 3.313 × 10-27 J

So, the energy (E2) of the oscillatory wave with a frequency of approximately 4,986,111.11 Hz and a 1° phase shift is also approximately 3.313 × 10-27 Joules.

To determine the infinitesimal loss of energy (&Delt

Where, h is Planck's constant (6.626 × 10-34 J·s), f2 is the new frequency (approximately) 4,986,111.11 Hz.

Δt is the infinitesimal time interval, which corresponds to the phase shift.

Known that the time shift resulting from a 1° phase shift is approximately 555 picoseconds (ps)

So, Δt=555 ps=555 × 10-12 s. Now, calculate ΔE.

ΔE=(6.626 × 10-34 J·s) × (4,986,111.11 Hz) × (555 × 10-12 s) ≈ 1.848 × 10-27 J

So, the infinitesimal loss of energy (ΔE) due to the 1° phase shift is approximately 1.848 × 10-27 Joules.

Resolved, the energy (E2) of this oscillatory wave is approximately 3.313 × 10-27 Joules. Resolved, the infinitesimal loss of energy (ΔE) due to the 1° phase shift is approximately

1.848 × 10-27 Joules.

Resolved, the resulting frequency (f2) of the oscillatory wave with a 1° phase shift is approximately 4,986,111.11 Hz.

Entity descriptions

In this section, we provide detailed descriptions of essential entities central to the study of phase shift, time intervals, and frequencies. These entities are fundamental to understanding wave behaviour and its practical applications.

Phase shift entities:

• Phase shift T(deg): This entity represents the angular displacement between two waveforms due to a shift in time or space, typically measured in degrees (°) or radians (rad).

• Periodic waveform or signal (f1): Refers to the waveform or undergoing the phase shift analysis.

Time shift (Δt): Denotes the temporal difference or distortion between corresponding points on two waveforms, resulting from a phase shift.

Reference waveform or signal (f2, t0): Represents the original waveform or signal serving as a reference for comparison when measuring phase shift.

veform or signal serving as a reference for comparison when measuring phase shift.

Time interval (T): Signifies the duration required for one complete cycle of the waveform.

Frequency (f): Denotes the number of cycles per unit time, typically measured in hertz (Hz).

Time or angle units (Δt, θ): The units used to express the phase shift, which can be either time units (e.g., seconds, Δt) or angular units (degrees, θ, or radians, θ).

Time delay (Δt): Represents the time difference introduced by the phase shift, influencing the temporal alignment of waveforms.

Frequency difference (Δf): Signifies the disparity in frequency between two waveforms undergoing phase shift.

Phase angle (Φ°): Quantifies the angular measurement that characterizes the phase shift between waveforms.

Relationship between phase shift, time interval, and frequency entities:

Time interval for 1° phase shift T(deg): Represents the time required for a 1° phase shift and is inversely proportional to frequency, playing a pivotal role in phase shift analysis.

Time distortion (Δt): Corresponds to the temporal shift induced by a 1° phase shift and is calculated based on the time interval for 1° of phase shift T(deg) and frequency (f).

Angular displacement (ΔΦ): Denotes the angular difference between corresponding points on two waveforms, providing insight into phase shift.

Wavelength and speed of propagation entities:

Wavelength (λ): Signifies the distance between two corresponding points on a waveform, a crucial parameter dependent on the speed of propagation (c) and frequency (f).

Speed of propagation (c): Represents the velocity at which the waveform propagates through a specific medium, impacting the wavelength in wave propagation.

Time distortion and infinitesimal loss of wave energy entities:

Time distortion (Δt): Quantifies the temporal shift caused by a 1° phase shift, critical in scenarios requiring precise timing and synchronization.

Infinitesimal loss of wave energy (ΔE): Denotes the minuscule reduction in wave energy due to various factors, including phase shift, with equations provided to calculate these losses.

These entity descriptions serve as the foundation for comprehending phase shift analysis, time intervals, frequency relationships, and the quantification of infinitesimal wave energy loss. They are instrumental in both theoretical analyses and practical applications involving wave phenomena, offering clarity and precision in understanding the complex behaviour of waves.

Discussion

The research conducted on phase shift and infinitesimal wave energy loss equations has yielded profound insights into wave behaviour, phase analysis, and the consequences of phase shifts. This discussion section delves into the critical findings and their far-reaching implications.

Understanding phase shift

Our research has illuminated the central role of phase shift, a measure of angular displacement between waveforms, in understanding wave phenomena. Typically quantified in degrees (°) or radians (rad), phase shift analysis has emerged as a fundamental tool across multiple scientific and engineering domains. It enables researchers and engineers to precisely measure and manipulate the temporal or spatial relationship between waveforms.

The power of equations

The heart of our research lies in the development of fundamental equations that underpin phase shift analysis and energy loss calculations. The phase angle equations (Φ°=360° × f × Δt, Δt=Φ°/ (360° × f), and f=Φ°/(360° × Δt)) provide a robust framework for relating phase angle, frequency, and time delay. These equations are indispensable tools for quantifying and predicting phase shifts with accuracy.

Inversely proportional time interval

One of the pivotal findings of our research is the inverse relationship between the time interval for a 1° phase shift (T(deg)) and the frequency (f) of the waveform. This discovery, encapsulated in T(deg) ∝ 1/f, underscores the critical role of frequency in determining the extent of phase shift. As frequency increases, the time interval for a 1° phase shift decreases proportionally. This insight has profound implications in fields such as telecommunications, where precise timing and synchronization are paramount.

Wavelength and propagation speed

Our research underscores the significance of wavelength (λ) in understanding wave propagation. The equation λ=c/f highlights that wavelength depends on the speed of propagation (c) and frequency (f). Diverse mediums possess distinct propagation speeds, impacting the wavelength of waves as they traverse various environments. This knowledge is invaluable in comprehending phenomena such as electromagnetic wave propagation through materials with varying properties.

Time distortion and its implications

We introduce the concept of time distortion (Δt), representing the temporal shifts induced by a 1° phase shift. This concept is particularly relevant in scenarios where precise timing is critical, as exemplified in telecommunications, radar systems, and precision instruments like atomic clocks. Understanding the effects of time distortion allows for enhanced accuracy in time measurement and synchronization.

Infinitesimal wave energy loss

Our research extends to the nuanced topic of infinitesimal wave energy loss (ΔE), which can result from various factors, including phase shift. The equations ΔE=hfΔt, ΔE=(2πhf1/360) × T(deg), and ΔE=(2πh/360) × T(deg) × (1/Δt) offer a means to calculate these energy losses. This concept is indispensable in fields such as quantum mechanics, where energy transitions are fundamental to understanding the behaviour of particles and systems.

Applications in science and engineering

Phase shift analysis, as elucidated in our research, finds extensive applications across diverse scientific and engineering disciplines. From signal processing and electromagnetic wave propagation to medical imaging and quantum mechanics, the ability to quantify and manipulate phase shift is pivotal for advancing knowledge and technology. Additionally, understanding infinitesimal wave energy loss is crucial in optimizing the efficiency of systems and devices across various domains.

Our research on phase shift and infinitesimal wave energy loss equations has illuminated the fundamental principles governing wave behaviour and its practical applications. By providing a comprehensive framework for phase shift analysis and energy loss calculations, this research contributes to the advancement of scientific understanding and technological innovation in a wide array of fields. These findings have the potential to reshape how we harness the power of waves and enhance precision in a multitude of applications.

In this comprehensive exploration of phase shift and infinitesimal wave energy loss equations, our research has unveiled a of knowledge that deepens our understanding of wave behaviour and its practical applications. This concluding section summarizes the key findings and underscores the significance of our work.

Unravelling phase shift

The focal point of our research has been the elucidation of phase shift, a fundamental concept in wave phenomena. We have demonstrated that phase shift analysis, quantified in degrees (°) or radians (rad), is a versatile tool with applications spanning diverse scientific and engineering domains. Phase shift allows us to precisely measure and manipulate the relative timing or spatial displacement of waveforms, providing valuable insights into wave behaviour.

The power of equations

At the heart of our research lies a set of fundamental equations that serve as the cornerstone for phase shift analysis and energy loss calculations. The phase angle equations (Φ°=360° × f × Δt, Δt=Φ°/(360° × f), and f=Φ°/(360° × Δt)) offer a robust mathematical framework for relating phase angle, frequency, and time delay. These equations empower researchers and engineers to quantify phase shifts with precision, driving advancements in fields where precise synchronization is paramount.

Time interval and frequency

One of the pivotal revelations of our research is the inverse relationship between the time interval for a 1° phase shift T(deg) and the frequency (f) of the waveform. Our findings, encapsulated in T(deg) ∝ 1/f, underscore the critical role of frequency in determining the extent of phase shift. This insight has profound implications for fields such as telecommunications, where precise timing and synchronization are foundational.

Wavelength and propagation speed

Our research has underscored the significance of wavelength (λ) in understanding wave propagation. The equation λ=c/f has revealed that wavelength depends on the speed of propagation (c) and frequency (f). This knowledge is indispensable for comprehending wave behaviour in diverse mediums and has practical applications in fields ranging from optics to telecommunications.

Time distortion's important role

We introduced the concept of time distortion (Δt), which represents the temporal shifts induced by a 1° phase shift. This concept is particularly relevant in scenarios where precise timing is essential, such as in telecommunications, radar systems, and precision instruments like atomic clocks. Understanding the effects of time distortion enhances our ability to measure and control time with unprecedented accuracy.

Infinitesimal wave energy loss

Our research delved into the nuanced topic of infinitesimal wave energy loss (ΔE), which can result from various factors, including phase shift. The equations ΔE=hfΔt, ΔE=(2πhf1/360) × T(deg), and ΔE=(2πh/360) × T(deg) × (1/Δt) provide a robust framework for calculating these energy losses. This concept is instrumental in fields such as quantum mechanics, where precise control of energy transitions is central to understanding the behaviour of particles and systems.

Applications across disciplines

Phase shift analysis, as elucidated in our research, finds extensive applications across diverse scientific and engineering disciplines. From signal processing and electromagnetic wave propagation to medical imaging and quantum mechanics, the ability to quantify and manipulate phase shift has far- reaching implications for advancing knowledge and technology. Additionally, understanding infinitesimal wave energy loss is crucial for optimizing the efficiency of systems and devices in various domains.

Conclusion

In conclusion, our research on phase shift and infinitesimal wave energy loss equations has not only enriched our understanding of wave behaviour but also facilitated the progression for innovative applications across multiple fields. These findings have the potential to reshape how we exploit the potential energy of waves, enhance precision, and drive advancements in science and technology. As we move forward, the insights gained from this research will continue to inspire new discoveries and innovations, ultimately benefiting society as a whole.

References

1. NIST. Time and frequency from A to Z, P. 2023.
2. Thakur SN, Samal P, Bhattacharjee D. Relativistic effects on phaseshift in frequencies invalidate time dilation II. TechRxiv. 2023.

   [Crossref] [Google Scholar]

3. Urone PP. wave properties: speed, amplitude, frequency, and period. In Physics. 2020.
4. Smith JD. Fundamentals of Wave Behaviour. Phys Today. 2005;58(7):42-47.
5. Boiko J, Tolubko V, Barabash O, Eromenko O, Havrylko Y. Signal processing with frequency and phase shift keying modulation in telecommunications. Telkomnika. 2019;17(4):2025-2038.

   [Crossref] [Google Scholar]

6. Eleuch H, Rotter I. Gain and loss in open quantum systems. Phys Rev E. 2017;95(6):062109.

   [Crossref] [Google Scholar]

7. Debnath SK, Park Y. Real-time quantitative phase imaging with a spatial phase-shifting algorithm. Opt Lett. 2011;36(23):4677-4679.

   [Crossref] [Google Scholar]

8. Wiesbeck W, Sit L. Radar 2020: The future of radar systems. In 2014 International Radar Conference. IEEE. 2014:1-6.

   [Crossref] [Google Scholar]

Author Info

Soumendra Nath Thakur1* and Deep Bhattacharjee2

 

1Department of Computer Science and Engineering, Tagore's Electronic Lab, Kolkata, West Bengal, India

2Department of Physics, Electro-Gravitational Space Propulsion Laboratory, Integrated Nanosciences Research, Kanpur, India

 

Citation: Thakur SN, Bhattacharjee D (2023) Phase Shift and Infinitesimal Wave Energy Loss Equations. J Phys Chem Biophys. 13:365.

Received: 28-Sep-2023, Manuscript No. JPCB-23-27248; Editor assigned: 02-Oct-2023, Pre QC No. JPCB-23-27248 (PQ); Reviewed: 16-Oct-2023, QC No. JPCB-23-27248; Revised: 23-Oct-2023, Manuscript No. JPCB-23-27248 (R); Published: 30-Oct-2023 , DOI: 10.35248/2161-0398.23.13.365

Copyright: © 2023 Thakur SN, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Cite:

Thakur, S. N., & Bhattacharjee, D. (2023b). Phase shift and infinitesimal wave energy loss equations. Journal of Physical Chemistry & Biophysics, 13(6), JPCB-23-27248 (R). https://doi.org/10.13140/RG.2.2.28013.97763 https://www.longdom.org/open-access/phase-shift-and-infinitesimal-wave-energy-loss-equations-104719.html BibTeX @article{thakur-2023, author = {Thakur, Soumendra Nath and Bhattacharjee, Deep}, journal = {Journal of Physical Chemistry & Biophysics}, month = {10}, number = {6}, pages = {1--6}, title = {{Phase shift and infinitesimal wave energy loss equations}}, volume = {13}, year = {2023}, doi = {10.13140/RG.2.2.28013.97763}, url = {https://www.longdom.org/open-access/phase-shift-and-infinitesimal-wave-energy-loss-equations-104719.html}, } BibLaTeX @article{thakur-2023, author = {given-i=SN, given={Soumendra Nath}, family=Thakur and given-i=D, given=Deep, family=Bhattacharjee}, date = {2023-10-30}, doi = {10.13140/RG.2.2.28013.97763}, journaltitle = {Journal of Physical Chemistry & Biophysics}, number = {6}, pages = {1--6}, title = {Phase shift and infinitesimal wave energy loss equations}, url = {https://www.longdom.org/open-access/phase-shift-and-infinitesimal-wave-energy-loss-equations-104719.html}, volume = {13}, }