Phase Shift and Infinitesimal Wave Energy Loss Equations
Soumendra Nath Thakur1* and Deep Bhattacharjee2
*Correspondence: Soumendra Nath Thakur, Department of Computer Science and Engineering, Tagore's Electronic Lab, Kolkata, West Bengal, India, Email:
Abstract
The research paper provides a mathematical framework for understanding phase shift in wave phenomena, bridging theoretical foundations with real-world applications. It emphasizes the importance of phase shift in physics and engineering, particularly in fields like telecommunications and acoustics. Key equations are introduced to explain phase angle, time delay, frequency, and wavelength relationships. The study also introduces the concept of time distortion due to a 1° phase shift, crucial for precise time measurements in precision instruments. The research also addresses infinitesimal wave energy loss related to phase shift, enriching our understanding of wave behaviour and impacting scientific and engineering disciplines.
Keywords
Phase shift; Phase angle; Time distortion; Wave energy loss; Wave phenomena
Introduction
The study of phase shift in wave phenomena stands as a fundament in physics and engineering, playing an indispensable role in various applications. Phase shift refers to the phenomenon where a periodic waveform or signal appears displaced in time or space relative to a reference waveform or signal. This displacement, measured in degrees or radians, offers profound insights into the intricate behaviour of waves [1].
Phase shift analysis is instrumental in comprehending wave behaviour and is widely employed in fields such as telecommunications, signal processing, and acoustics, where precise timing and synchronization are paramount. The ability to quantify and manipulate phase shift is pivotal in advancing our understanding of wave phenomena and harnessing them for practical applications.
This research is dedicated to exploring the fundamental principles of phase shift, unravelling its complexities, and establishing a clear framework for analysis. It places a spotlight on essential entities, including waveforms, reference points, frequencies, and units, which are critical in conducting precise phase shift calculations. The presentation of key equations further enhances our grasp of the relationships between phase angle, time delay, frequency, and wavelength, illuminating the intricate mechanisms governing wave behaviour [2].
Moreover, this research introduces the concept of time distortion, which encapsulates the temporal shifts induced by a 1° phase shift. This concept is especially relevant when considering phase shift effects in real-world scenarios, particularly in precision instruments like clocks and radar systems.
In addition to phase shift, this research addresses the topic of infinitesimal wave energy loss and its close association with phase shift. It provides a set of equations designed to calculate energy loss under various conditions, taking into account factors such as phase shift, time distortion, and source frequencies. These equations expand our understanding of how phase shift influences wave energy, emphasizing its practical implications.
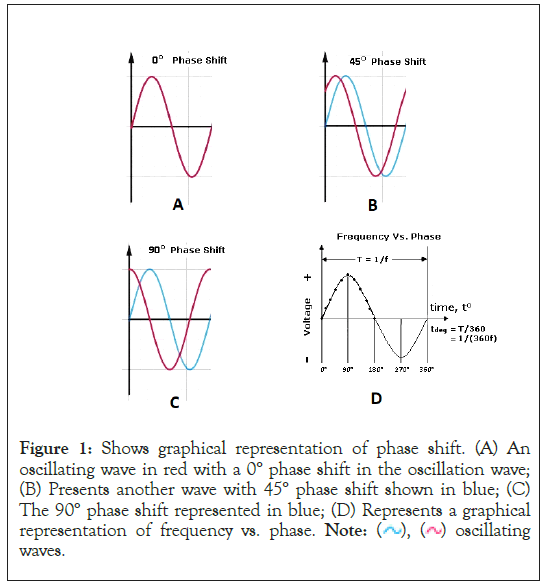
In summary, this research paper endeavours to offer a comprehensive exploration of phase shift analysis, bridging the gap between theoretical foundations and practical applications. By elucidating the complex connections between phase shift, time, frequency, and energy, this study enriches our comprehension of wave behaviour across a spectrum of scientific and engineering domains (Figure 1).
Figure 1: Shows graphical representation of phase shift. (A) An oscillating wave in red with a 0° phase shift in the oscillation wave; (B) Presents another wave with 45° phase shift shown in blue; (C) The 90° phase shift represented in blue; (D) Represents a graphical representation of frequency vs. phase. Note:  oscillating waves.
oscillating waves.
Materials and Methods
Relationship between phase shift, time interval, frequency and time delay
The methodological approach in this research involves the formulation and derivation of fundamental equations related to phase shift analysis. These equations establish the relationships between phase shift T(deg), time interval (T), time delay (Δt), frequency (f), and wavelength (λ) in wave phenomena. The derived equations include:
• T(deg) ∝ 1/f-this equation establishes the inverse proportionality between the time interval for 1° of phase shift T(deg) and frequency (f).
• 1° phase shift=T/360-expresses the relationship between 1° phase shift and time interval (T).
• 1° phase shift=T/360=(1/f)/360-further simplifies the equation for 1° phase shift, revealing its dependence on frequency.
• T(deg)=(1/f)/360-provides a direct formula for calculating T(deg) based on frequency, which can be invaluable in phase shift analysis.
• Time delay (Δt)=T(deg)=(1/f)/360-expresses time delay (or time distortion) in terms of phase shift and frequency.
Formulation of phase shift equations
The methodological approach in this research involves the formulation and derivation of fundamental equations related to phase shift analysis. These equations establish the relationships between phase angle (Φ°), time delay (Δt), frequency (f), and wavelength (λ) in wave phenomena. The equations developed are:
• Φ°=360° × f × Δt-this equation relates the phase angle in degrees to the product of frequency and time delay, providing a fundamental understanding of phase shift.
• Δt=Φ°/(360° × f)-this equation expresses the time delay (or time distortion) in terms of the phase angle and frequency, elucidating the temporal effects of phase shift.
• f=Φ°/(360° × Δt)-this equation allows for the determination of frequency based on the phase angle and time delay, contributing to frequency analysis.
• λ=c/f-the wavelength equation calculates the wavelength (λ) using the speed of propagation (c) and frequency (f), applicable to wave propagation through different media [3].
Relevant equations
The research paper on phase shift analysis and related concepts provides a set of equations that play a central role in understanding phase shift, time intervals, frequency, and their interrelationships. These equations are fundamental to the study of wave phenomena and their practical applications. Here are the relevant equations presented in the research.
Phase shift equations: Relationship between phase shift, time interval, and frequency.
These equations describe the connection between phase shift, time interval (T), and frequency (f).
• T(deg) ∝ 1/f-indicates the inverse proportionality between the time interval for 1° of phase shift T(deg) and frequency (f).
• 1° phase shift=T/360-relates 1° phase shift to time interval (T).
• 1° phase shift=T/360=(1/f)/360-simplifies the equation for 1° phase shift, emphasizing its dependence on frequency.
• T(deg)=(1/f)/360-provides a direct formula for calculating T(deg) based on frequency.
Phase angle equations
These equations relate phase angle (Φ°) to frequency (f) and time delay (Δt), forming the core of phase shift analysis.
• Φ°=360° × f × Δt-this equation defines the phase angle (in degrees) as the product of frequency and time delay.
• Δt=Φ°/(360° × f)-expresses time delay (or time distortion) in terms of phase angle and frequency.
• f=Φ°/(360° × Δt)-allows for the calculation of frequency based on phase angle and time delay.
Wavelength equation
This equation calculates the wavelength (λ) based on the speed of propagation (c) and frequency (f).
λ=c/f
The wavelength (λ) is determined by the speed of propagation (c) and the frequency (f) of the wave.
Time distortion equation
This equation quantifies the time shift caused by a 1° phase shift and is calculated based on the time interval for 1° of phase shift T(deg), which is inversely proportional to frequency (f).
• Time Distortion (Δt)=T(deg)=(1/f)/360-expresses the time distortion (Δt) as a function of T(deg) and frequency (f).
Infinitesimal loss of wave energy equations
These equations relate to the infinitesimal loss of wave energy (ΔE) due to various factors, including phase shift.
• ΔE=hfΔt-calculates the infinitesimal loss of wave energy (ΔE) based on Planck's constant (h), frequency (f), and time distortion (Δt).
• ΔE=(2πhf1/360) × T(deg)-determines ΔE when source frequency (f1) and phase shift T(deg) are known.
• ΔE=(2πh/360) × T(deg) × (1/Δt)-calculates ΔE when phase shift T(deg) and time distortion (Δt) are known.
These equations collectively form the foundation for understanding phase shift analysis, time intervals, frequency relationships, and the quantification of infinitesimal wave energy loss. They are instrumental in both theoretical analyses and practical applications involving wave phenomena [4,5].
Results
This section introduces two key concepts that deepen our understanding of wave behaviour and its practical implications: Time distortion and infinitesimal loss of wave energy. These concepts focus on the temporal aspects of phase shift and offer valuable insights into the energy dynamics of wave phenomena.
Time distortion
The concept of time distortion (Δt) is a pivotal bridge between phase shift analysis and precise time measurements, particularly in applications where accuracy is paramount. Time distortion represents the temporal shift that occurs as a consequence of a 1° phase shift in a wave.
Consider a 5 MHz wave as an example. A 1° phase shift on this wave corresponds to a time shift of approximately 555 picoseconds (ps). In other words, when a wave experiences a 1° phase shift, specific events or points on the waveform appear displaced in time by this minuscule but significant interval.
Time distortion is a crucial consideration in various fields, including telecommunications, navigation systems, and scientific instruments. Understanding and quantifying this phenomenon enables scientists and engineers to make precise time measurements and synchronize systems accurately [6].
Infinitesimal loss of wave energy
In addition to time distortion, this research delves into the intricacies of infinitesimal wave energy loss (ΔE) concerning phase shift. It provides a framework for quantifying the diminutive energy losses experienced by waves as a result of various factors, with phase shift being a central element.
The equations presented in this research allow for the calculation of ΔE under different scenarios. These scenarios consider parameters such as phase shift, time distortion, and source frequencies. By understanding how phase shift contributes to energy loss, researchers and engineers gain valuable insights into the practical implications of this phenomenon.
Infinitesimal wave energy loss has implications in fields ranging from quantum mechanics to telecommunications. It underlines the importance of precision in wave-based systems and highlights the trade-offs between manipulating phase for various applications and conserving wave energy.
In summary, this section serves as an introduction to the intricate concepts of time distortion and infinitesimal loss of wave energy. These concepts provide a more comprehensive picture of wave behaviour, offering practical tools for precise measurements and energy considerations in diverse scientific and engineering domains [7,8].
Phase shift calculations and example
To illustrate the practical application of the derived equations of phase shift T(deg), an example calculation is presented:
Phase Shift Example 1:1° Phase Shift on a 5 MHz Wave.
The calculation demonstrates how to determine the time shift caused by a 1° phase shift on a 5 MHz wave. It involves substituting the known frequency (f=5 MHz) into the equation for T(deg).
T(deg)=(1/f)/360; f=5 MHz (5,000,000 Hz)
Now, plug in the frequency (f) into the equation for T(deg).
T(deg)={1/(5,000,000 Hz)}/360
Calculate the value of T(deg).
T(deg) ≈ 555 picoseconds (ps)
So, a 1° phase shift on a 5 MHz wave corresponds to a time shift of approximately 555 picoseconds (ps).
Loss of wave energy calculations and example
Loss of wave energy example 1: To illustrate the practical applications of the derived equations of loss of wave energy, example calculation is presented.
Oscillation frequency 5 MHz, when 0° Phase shift in frequency
This calculation demonstrate how to determine the energy (E1) and infinitesimal loss of energy (ΔE) of an oscillatory wave, whose frequency (f1) is 5 MHz, and Phase shift T(deg)=0° (i.e. no phase shift).
To determine the energy (E1) and infinitesimal loss of energy (ΔE) of an oscillatory wave with a frequency (f1) of 5 MHz and a phase shift T(deg) of 0°, use the following equations:
Calculate the energy (E1) of the oscillatory wave:
E1=hf1
Where, h is Planck's constant ≈ 6.626 × 10-34 J·s, f1 is the frequency of the wave, which is 5 MHz (5 × 106 Hz). E1={6.626 × 10-34 J·s} × (5 × 106 Hz)=3.313 × 10-27 J
So, the energy (E1) of the oscillatory wave is approximately 3.313 × 10-27 Joules. To determine the infinitesimal loss of energy (ΔE), use the formula
ΔE=hfΔt
Where, h is Planck's constant {6.626 × 10-34 J·s}, f1 is the frequency of the wave (5 × 106 Hz).
Δt is the infinitesimal time interval, and in this case, since there's no phase shift, T(deg)=0°, Δt=0.
ΔE={6.626 × 10-34 J·s} × (5 × 106 Hz) × 0=0 (Joules)
The infinitesimal loss of energy (ΔE) is 0 joules because there is no phase shift, meaning there is no energy loss during this specific time interval.
Resolved, the energy (E₁) of the oscillatory wave with a frequency of 5 MHz and no phase shift is approximately 3.313 × 10-27 Joules.
There is no infinitesimal loss of energy (ΔE) during this specific time interval due to the absence of a phase shift.
Loss of wave energy example 2: To illustrate the practical applications of the derived equations of loss of wave energy, example calculation is presented.
Original oscillation frequency 5 MHz, when 1° Phase shift compared to original frequency.
This calculation demonstrate how to determine the energy (E2) and infinitesimal loss of energy (ΔE) of another oscillatory wave, compared to the original frequency (f1) of 5 MHz and Phase shift T(deg)=1°, resulting own frequency (f2).
To determine the energy (E2) and infinitesimal loss of energy (ΔE) of another oscillatory wave with a 1° phase shift compared to the original frequency (f1) of 5 MHz, and to find the resulting frequency (f2) of the wave, follow these steps:
Calculate the energy (E2) of the oscillatory wave with the new frequency (f2) using the Planck's energy formula.
E2=hf2
Where, h is Planck's constant ≈ 6.626 × 10-34 J·s, f2 is the new frequency of the wave.
Calculate the change in frequency (Δf2) due to the 1° phase shift: Δf2=(1°/360°) × f1
Where, 1° is the phase shift, 360° is the full cycle of phase.
f₁ is the original frequency, which is 5 MHz (5 × 106 Hz). Δf2=(1/360) × (5
Now that you have Δf2, you can calculate the new frequency (f2): f2=f1-Δf2
f2=(5 × 106 Hz)-(13,888.89 Hz) ≈ 4,986,111.11 Hz
So, the resulting frequency (f2) of the oscillatory wave with a 1° phase shift is approximately 4,986,111.11 Hz.
Calculate the energy (E2) using the new frequency (f2).
E2=hf2
E2 ≈ (6.626 × 10-34 J·s) × (4,986,111.11 Hz) ≈ 3.313 × 10-27 J
So, the energy (E2) of the oscillatory wave with a frequency of approximately 4,986,111.11 Hz and a 1° phase shift is also approximately 3.313 × 10-27 Joules.
To determine the infinitesimal loss of energy (&Delt
Where, h is Planck's constant (6.626 × 10-34 J·s), f2 is the new frequency (approximately) 4,986,111.11 Hz.
Δt is the infinitesimal time interval, which corresponds to the phase shift.
Known that the time shift resulting from a 1° phase shift is approximately 555 picoseconds (ps)
So, Δt=555 ps=555 × 10-12 s. Now, calculate ΔE.
ΔE=(6.626 × 10-34 J·s) × (4,986,111.11 Hz) × (555 × 10-12 s) ≈ 1.848 × 10-27 J
So, the infinitesimal loss of energy (ΔE) due to the 1° phase shift is approximately 1.848 × 10-27 Joules.
Resolved, the energy (E2) of this oscillatory wave is approximately 3.313 × 10-27 Joules. Resolved, the infinitesimal loss of energy (ΔE) due to the 1° phase shift is approximately
1.848 × 10-27 Joules.
Resolved, the resulting frequency (f2) of the oscillatory wave with a 1° phase shift is approximately 4,986,111.11 Hz.
Entity descriptions
In this section, we provide detailed descriptions of essential entities central to the study of phase shift, time intervals, and frequencies. These entities are fundamental to understanding wave behaviour and its practical applications.
Phase shift entities:
• Phase shift T(deg): This entity represents the angular displacement between two waveforms due to a shift in time or space, typically measured in degrees (°) or radians (rad).
• Periodic waveform or signal (f1): Refers to the waveform or undergoing the phase shift analysis.
Time shift (Δt): Denotes the temporal difference or distortion between corresponding points on two waveforms, resulting from a phase shift.
Reference waveform or signal (f2, t0): Represents the original waveform or signal serving as a reference for comparison when measuring phase shift.
veform or signal serving as a reference for comparison when measuring phase shift.
Time interval (T): Signifies the duration required for one complete cycle of the waveform.
Frequency (f): Denotes the number of cycles per unit time, typically measured in hertz (Hz).
Time or angle units (Δt, θ): The units used to express the phase shift, which can be either time units (e.g., seconds, Δt) or angular units (degrees, θ, or radians, θ).
Time delay (Δt): Represents the time difference introduced by the phase shift, influencing the temporal alignment of waveforms.
Frequency difference (Δf): Signifies the disparity in frequency between two waveforms undergoing phase shift.
Phase angle (Φ°): Quantifies the angular measurement that characterizes the phase shift between waveforms.
Relationship between phase shift, time interval, and frequency entities:
Time interval for 1° phase shift T(deg): Represents the time required for a 1° phase shift and is inversely proportional to frequency, playing a pivotal role in phase shift analysis.
Time distortion (Δt): Corresponds to the temporal shift induced by a 1° phase shift and is calculated based on the time interval for 1° of phase shift T(deg) and frequency (f).
Angular displacement (ΔΦ): Denotes the angular difference between corresponding points on two waveforms, providing insight into phase shift.
Wavelength and speed of propagation entities:
Wavelength (λ): Signifies the distance between two corresponding points on a waveform, a crucial parameter dependent on the speed of propagation (c) and frequency (f).
Speed of propagation (c): Represents the velocity at which the waveform propagates through a specific medium, impacting the wavelength in wave propagation.
Time distortion and infinitesimal loss of wave energy entities:
Time distortion (Δt): Quantifies the temporal shift caused by a 1° phase shift, critical in scenarios requiring precise timing and synchronization.
Infinitesimal loss of wave energy (ΔE): Denotes the minuscule reduction in wave energy due to various factors, including phase shift, with equations provided to calculate these losses.
These entity descriptions serve as the foundation for comprehending phase shift analysis, time intervals, frequency relationships, and the quantification of infinitesimal wave energy loss. They are instrumental in both theoretical analyses and practical applications involving wave phenomena, offering clarity and precision in understanding the complex behaviour of waves.
Discussion
The research conducted on phase shift and infinitesimal wave energy loss equations has yielded profound insights into wave behaviour, phase analysis, and the consequences of phase shifts. This discussion section delves into the critical findings and their far-reaching implications.
Understanding phase shift
Our research has illuminated the central role of phase shift, a measure of angular displacement between waveforms, in understanding wave phenomena. Typically quantified in degrees (°) or radians (rad), phase shift analysis has emerged as a fundamental tool across multiple scientific and engineering domains. It enables researchers and engineers to precisely measure and manipulate the temporal or spatial relationship between waveforms.
The power of equations
The heart of our research lies in the development of fundamental equations that underpin phase shift analysis and energy loss calculations. The phase angle equations (Φ°=360° × f × Δt, Δt=Φ°/ (360° × f), and f=Φ°/(360° × Δt)) provide a robust framework for relating phase angle, frequency, and time delay. These equations are indispensable tools for quantifying and predicting phase shifts with accuracy.
Inversely proportional time interval
One of the pivotal findings of our research is the inverse relationship between the time interval for a 1° phase shift (T(deg)) and the frequency (f) of the waveform. This discovery, encapsulated in T(deg) ∝ 1/f, underscores the critical role of frequency in determining the extent of phase shift. As frequency increases, the time interval for a 1° phase shift decreases proportionally. This insight has profound implications in fields such as telecommunications, where precise timing and synchronization are paramount.
Wavelength and propagation speed
Our research underscores the significance of wavelength (λ) in understanding wave propagation. The equation λ=c/f highlights that wavelength depends on the speed of propagation (c) and frequency (f). Diverse mediums possess distinct propagation speeds, impacting the wavelength of waves as they traverse various environments. This knowledge is invaluable in comprehending phenomena such as electromagnetic wave propagation through materials with varying properties.
Time distortion and its implications
We introduce the concept of time distortion (Δt), representing the temporal shifts induced by a 1° phase shift. This concept is particularly relevant in scenarios where precise timing is critical, as exemplified in telecommunications, radar systems, and precision instruments like atomic clocks. Understanding the effects of time distortion allows for enhanced accuracy in time measurement and synchronization.
Infinitesimal wave energy loss
Our research extends to the nuanced topic of infinitesimal wave energy loss (ΔE), which can result from various factors, including phase shift. The equations ΔE=hfΔt, ΔE=(2πhf1/360) × T(deg), and ΔE=(2πh/360) × T(deg) × (1/Δt) offer a means to calculate these energy losses. This concept is indispensable in fields such as quantum mechanics, where energy transitions are fundamental to understanding the behaviour of particles and systems.
Applications in science and engineering
Phase shift analysis, as elucidated in our research, finds extensive applications across diverse scientific and engineering disciplines. From signal processing and electromagnetic wave propagation to medical imaging and quantum mechanics, the ability to quantify and manipulate phase shift is pivotal for advancing knowledge and technology. Additionally, understanding infinitesimal wave energy loss is crucial in optimizing the efficiency of systems and devices across various domains.
Our research on phase shift and infinitesimal wave energy loss equations has illuminated the fundamental principles governing wave behaviour and its practical applications. By providing a comprehensive framework for phase shift analysis and energy loss calculations, this research contributes to the advancement of scientific understanding and technological innovation in a wide array of fields. These findings have the potential to reshape how we harness the power of waves and enhance precision in a multitude of applications.
In this comprehensive exploration of phase shift and infinitesimal wave energy loss equations, our research has unveiled a of knowledge that deepens our understanding of wave behaviour and its practical applications. This concluding section summarizes the key findings and underscores the significance of our work.
Unravelling phase shift
The focal point of our research has been the elucidation of phase shift, a fundamental concept in wave phenomena. We have demonstrated that phase shift analysis, quantified in degrees (°) or radians (rad), is a versatile tool with applications spanning diverse scientific and engineering domains. Phase shift allows us to precisely measure and manipulate the relative timing or spatial displacement of waveforms, providing valuable insights into wave behaviour.
The power of equations
At the heart of our research lies a set of fundamental equations that serve as the cornerstone for phase shift analysis and energy loss calculations. The phase angle equations (Φ°=360° × f × Δt, Δt=Φ°/(360° × f), and f=Φ°/(360° × Δt)) offer a robust mathematical framework for relating phase angle, frequency, and time delay. These equations empower researchers and engineers to quantify phase shifts with precision, driving advancements in fields where precise synchronization is paramount.
Time interval and frequency
One of the pivotal revelations of our research is the inverse relationship between the time interval for a 1° phase shift T(deg) and the frequency (f) of the waveform. Our findings, encapsulated in T(deg) ∝ 1/f, underscore the critical role of frequency in determining the extent of phase shift. This insight has profound implications for fields such as telecommunications, where precise timing and synchronization are foundational.
Wavelength and propagation speed
Our research has underscored the significance of wavelength (λ) in understanding wave propagation. The equation λ=c/f has revealed that wavelength depends on the speed of propagation (c) and frequency (f). This knowledge is indispensable for comprehending wave behaviour in diverse mediums and has practical applications in fields ranging from optics to telecommunications.
Time distortion's important role
We introduced the concept of time distortion (Δt), which represents the temporal shifts induced by a 1° phase shift. This concept is particularly relevant in scenarios where precise timing is essential, such as in telecommunications, radar systems, and precision instruments like atomic clocks. Understanding the effects of time distortion enhances our ability to measure and control time with unprecedented accuracy.
Infinitesimal wave energy loss
Our research delved into the nuanced topic of infinitesimal wave energy loss (ΔE), which can result from various factors, including phase shift. The equations ΔE=hfΔt, ΔE=(2πhf1/360) × T(deg), and ΔE=(2πh/360) × T(deg) × (1/Δt) provide a robust framework for calculating these energy losses. This concept is instrumental in fields such as quantum mechanics, where precise control of energy transitions is central to understanding the behaviour of particles and systems.
Applications across disciplines
Phase shift analysis, as elucidated in our research, finds extensive applications across diverse scientific and engineering disciplines. From signal processing and electromagnetic wave propagation to medical imaging and quantum mechanics, the ability to quantify and manipulate phase shift has far- reaching implications for advancing knowledge and technology. Additionally, understanding infinitesimal wave energy loss is crucial for optimizing the efficiency of systems and devices in various domains.
Conclusion
In conclusion, our research on phase shift and infinitesimal wave energy loss equations has not only enriched our understanding of wave behaviour but also facilitated the progression for innovative applications across multiple fields. These findings have the potential to reshape how we exploit the potential energy of waves, enhance precision, and drive advancements in science and technology. As we move forward, the insights gained from this research will continue to inspire new discoveries and innovations, ultimately benefiting society as a whole.
References
- NIST. Time and frequency from A to Z, P. 2023.
- Thakur SN, Samal P, Bhattacharjee D. Relativistic effects on phaseshift in frequencies invalidate time dilation II. TechRxiv. 2023.
- Urone PP. wave properties: speed, amplitude, frequency, and period. In Physics. 2020.
- Smith JD. Fundamentals of Wave Behaviour. Phys Today. 2005;58(7):42-47.
- Boiko J, Tolubko V, Barabash O, Eromenko O, Havrylko Y. Signal processing with frequency and phase shift keying modulation in telecommunications. Telkomnika. 2019;17(4):2025-2038.
- Eleuch H, Rotter I. Gain and loss in open quantum systems. Phys Rev E. 2017;95(6):062109.
- Debnath SK, Park Y. Real-time quantitative phase imaging with a spatial phase-shifting algorithm. Opt Lett. 2011;36(23):4677-4679.
- Wiesbeck W, Sit L. Radar 2020: The future of radar systems. In 2014 International Radar Conference. IEEE. 2014:1-6.
Author Info
Citation: Thakur SN, Bhattacharjee D (2023) Phase Shift and Infinitesimal Wave Energy Loss Equations. J Phys Chem Biophys. 13:365.
Received: 28-Sep-2023, Manuscript No. JPCB-23-27248; Editor assigned: 02-Oct-2023, Pre QC No. JPCB-23-27248 (PQ); Reviewed: 16-Oct-2023, QC No. JPCB-23-27248; Revised: 23-Oct-2023, Manuscript No. JPCB-23-27248 (R); Published: 30-Oct-2023 , DOI: 10.35248/2161-0398.23.13.365
Copyright: © 2023 Thakur SN, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.